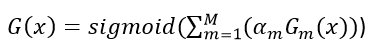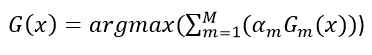....

Boosting

Classification

Decision Tree

Ensemble Technique

Machine Learning

Regression

January 14, 2021

Explain the step by step implementation of ADA Boost.

Let’s say we have AdaBoost model with M trees that has to be trained on a dataset with N rows. We have use this model for a binary classification problem with target variable having values {1,-1}. Following are the steps that are taken by AdaBoost algorithm:

1. Initialize weights for each observation with value of weight for any observation, say w_i a, being 1/N. This step would be executed only for the first tree in the sequence. For second tree onwards the algorithm would itself assign weights, the process for which is described in step 5.
2. Fit the tree, say G(x), on the data and make predictions.
3. Compute the error using the following formula: 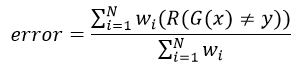where R(x)=1 , if condition is true i.e. G(x)  ≠ y, and 0 other wise. In other words numerator in above equation is only considered for wrong predictions.
4. Compute the contribution factor of the given tree, denoted by α, in a manner that the tree with higher performance gets higher value. The Following is the formula for calculating the contribution:
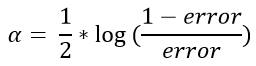
5. Compute the value of new weights in such a manner that the observations that were wrongly predicted by previous tree are highlighted i.e. given more weightage. Following is the formula for updating weights: 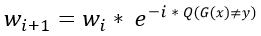where Q(x)=1 , if condition is true i.e. G(x)  ≠ y, and -1 other wise. In other words, wrong predictions are given higher values.
6. Go back to step 2 and repeat the process for remaining trees
7. Final predictions is made by aggregating the outputs of all the trees. Aggregation is done in a manner that preference is given to trees with higher performance. Following are the formulas for aggregating the output of of all trees in classification problems and regression problems respectively:

by : Monis Khan