Boosting

Ensemble Technique

Machine Learning

January 14, 2021

Explain the step by step implementation of Gradient Boosted Trees.

Gradient Boosted Trees predict the residuals instead of actual values. Thus the algorithm calculates the gradient of the given loss function and tries to find the minima i.e. where the value of loss function is minimum, hence highest accuracy. It can work with a variety of loss functions. AdaBoost is a special case of GBT that works with exponential loss function.

Following are the steps involved in training of GBT for a regression problem:

1. The algorithm starts with assuming the average of target column as prediction for all the observations. For subsequent trees the prediction value from step 6 is taken.
2. Fit the tree, say G(x), on the resulting dataset
3. Find the difference between actual values and the aforementioned average.
4. Calculate the average of each leaf node [voting in case of classification problem]. The resulting values form the first set of pseudo residuals
5. Take the pseudo residuals at the leaf nodes and calculate the hypothetical correct predictions for each leave node by subtracting the pseudo residual at that node from the older predicted value (prediction values from step 1)
6. Calculate the new set of predictions(for target value) using the following formula:
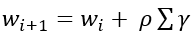
7. Return to step 1 and repeat the process for all the M trees.

For the sake of simplicity, here we’ve taken simple subtraction as loss function, but any other loss function would work just as well.

by : Monis Khan